문제
버블 소트 알고리즘을 다음과 같이 C++로 작성했다.
bool changed = false;
for (int i=1; i<=N+1; i++) {
changed = false;
for (int j=1; j<=N-i; j++) {
if (A[j] > A[j+1]) {
changed = true;
swap(A[j], A[j+1]);
}
}
if (changed == false) {
cout << i << '\n';
break;
}
}
위 소스에서 N은 배열의 크기이고, A는 정렬해야 하는 배열이다. 배열은 A[1]부터 사용한다.
위와 같은 소스를 실행시켰을 때, 어떤 값이 출력되는지 구해보자.
입력
첫째 줄에 N이 주어진다. N은 500,000보다 작거나 같은 자연수이다. 둘째 줄부터 N개의 줄에 A[1]부터 A[N]까지 하나씩 주어진다. A에 들어있는 수는 1,000,000보다 작거나 같은 자연수 또는 0이다.
출력
정답을 출력한다.
코드
#include<iostream>
#include<vector>
#include<algorithm>
#include<deque>
#include<stack>
#include<queue>
using namespace std;
int main()
{
int N;
cin >> N;
vector<pair<int, int>> A(N);
for (int i = 0; i <N; i++)
{
cin >> A[i].first;
A[i].second = i;
}
//A번 코드
sort(A.begin(), A.end());
int max = -1;
for (int i = 0; i < N; i++)
{
int min = A[i].second - i ;
if (min > max) max = min;
}
cout << max+1;
return 0;
}풀이
먼저 버블 정렬은 다음과 같다.

여기서 확인할 수 있는 것은
큰 수 일수록 오른쪽으로 밀려나가게 된다.
오름차순 정렬일 경우, 큰 순서대로 먼저 정렬이 된다.
확인하면 다음과 같다.
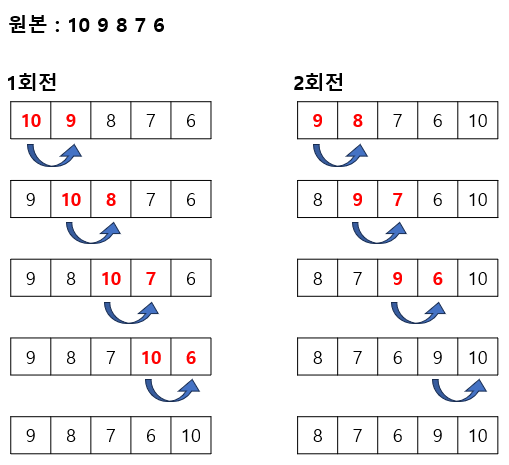
물론 3회전일 때는 8이 9왼쪽 으로 이동할 것 이고.
4회전일 때는 7이 8왼쪽으로 올 것 이다.
그럼 6은 몇번 이동할지 생각 해 보자.
1회전에서는 index 3
2회전에서는 index 2
3회전에서는 index 1
4회전에서는 index 0
총 4번 이동했다.
이 횟수는 버블 정렬의 회전 횟수와 동일하다.
왜냐하면 큰 수일수록, 오른쪽으로 한번에 자주 이동하는 경우가 많지만,
왼쪽으로 가는 경우 한 회전에 한번이다.
따라서 문제의 답변을 얻기 위해서는 왼쪽으로 간 횟수를 구하면 된다.
A번 설명
왼쪽으로 간 횟수 중 가장 큰 수가 회전 횟수 일 것 이다.
예를들면, 1이 맨 오른쪽에 있는 경우 왼쪽 숫자가 어쩌건 상관없이, 첫번째 인덱스로 즉 왼쪽으로 이동한 횟수가 가장 클 것이기 때문이고 이것이 회전 수 이기 때문이다.
그럼 왼쪽으로 얼마나 갔는지 어떻게 알 수 있을까?

바로 자신의 원본 index에서 현재 위치한 index를 차감시켜 주어야 얼마나 이동했는지 알 수 있다.
따라서 이동 횟수(회전 횟수)와 +1을 해야 문제에 대한 답변이 나온다.
왜냐하면 정렬이 완성된 회전 횟수에
완성이 되었는지 체크하는 코드가 있기 때문에
+1을 해주어야 한다.