백준 11004 k번째 수 [C++] 풀이 및 코드 (quick sort) 퀵 정렬 원리
문제
수 N개 A1, A2, ..., AN이 주어진다. A를 오름차순 정렬했을 때, 앞에서부터 K번째 있는 수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 N(1 ≤ N ≤ 5,000,000)과 K (1 ≤ K ≤ N)이 주어진다.
둘째에는 A1, A2, ..., AN이 주어진다. (-109 ≤ Ai ≤ 109)
출력
A를 정렬했을 때, 앞에서부터 K번째 있는 수를 출력한다.
코드
#include<iostream>
#include<vector>
#include<algorithm>
#include<deque>
#include<stack>
#include<queue>
#include<string>
using namespace std;
void quickSort(vector<int>& a, int s, int e, int k);
int partition(vector<int>& a, int s, int e);
void swap(vector<int>& a, int i, int j);
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n, k;
cin >> n >> k;
vector<int> arr(n, 0);
for (int i = 0; i < n; i++)
{
cin >> arr[i];
}
quickSort(arr, 0, n - 1, k-1);
cout << arr[k - 1];
return 0;
}
//B번
void quickSort(vector<int>& a, int s, int e, int k)
{
int pivot = partition(a, s, e);
if (pivot == k)
{
return;
}//B-2번
else if (k < pivot)
{
quickSort(a, s, pivot - 1, k);
}
else
{
quickSort(a, pivot + 1, e, k);
}
}
//A번
int partition(vector<int>& a, int s, int e)
{
int m = (s + e) / 2;
//A-1번
swap(a, s, m);
int pivot = a[s];
int i = s + 1, j = e;
while (i <= j)
{
while (j >= s + 1 && pivot < a[j])
{
j--;
}
while (i <= e && pivot > a[i])
{
i++;
}
//B-1번
if (i < j)
{
swap(a, i++, j--);
}
else
{
break;
}
}
a[s] = a[j];
a[j] = pivot;
return j;
}
void swap(vector<int>& a, int i, int j)
{
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}풀이
먼저 퀵 정렬의 원리를 문제에 적용하여 설명하겠습니다.
예제
5 2
4 1 2 3 5
퀵정렬은 데이터를 특정 기준으로 나누어 정렬을 하고 또 나누어 정렬하는 방법입니다.
그럼 4, 1, 2, 3, 5와 같은 예제나 다른 예제를 정렬하기 위해서 나누는 기준을 가운데로 하여 정렬을 하게 됩니다.
A번 설명
따라서 기준을 가운데로 하여 pivot을 지정합니다.
int m = (s + e) / 2;
하지만 이 pivot이 4, 1, 2, 3, 5라는 정수중에 가운데 값이 아닐 수 있습니다.
왜냐하면 해당 값중 중간 값은 3이기 때문이죠.
그럼 이 2를 기준으로 하기 위해서는 2의 왼쪽으로는 2보다 작은 수만, 2의 오른쪽은 2보다 큰 수만 오게 해야합니다.

그러기 위해서, pivot 즉 2보다 작은수와 큰수를 찾기위한 코드가 실행되어야 합니다.
A-1번 설명
tow pointer처럼, start와 end 포인터를 이용하여 pivot 즉 2보다 작거나 큰 수를 찾을 것 입니다.
start는 2보다 작은 수 인지 검사하는 포인터로,
end는 2보다 큰 수인지 검사하는 포인터로 사용합니다.
먼저 2를 가장 왼쪽으로 옮겨 start 위치를 잡기 쉽게 해줍시다.

이제 end 포인터가 pivot보다 큰 수인지 검사하게 되는데, 즉 2보다 작은 수를 찾는 역할입니다.

5그리고 3 그리고 4를 검사 해 보니 모두 2보다 큰 수 이기에 다른 기능을 수행하지 않아도 됩니다.

이렇게 start위치까지 오게 되면서, 마치게 되는데,
그럼 start를 확인 해 볼까요?

처음 1은 2보다 작으니 아무 기능을 수행하지 않을 것 입니다.
또한, end가 1에 이미 있으니 start에 포인터가 올라가면서 끝나게 됩니다.
끝으로 start가 end를 역전하는 상황이 오게 되는 것이죠.

이렇게 pivot을 기준으로 start와 end의 각 기능(큰 수 찾기와 작은 수 찾기)은 끝나게 됩니다.
끝으로 end와 pivot의 값을 swap해줍니다.

B번 설명
A번 코드 설명의 partition 함수에서 pivot index가 리턴되었습니다.
해당 index가 예제에서 찾는 k 즉 2번 index인지 확인하는 코드도 필요할 것 입니다.
int pivot = partition(a, s, e);
if (pivot == k)
{
return;
}따라서 해당 코드가 있고, 밑에는 재귀적으로 함수를 호출하여 다시 분열한 후 정렬하는 함수입니다.
그럼 다른 예제로 재귀적 호출을 이해 해 보겠습니다.
B-1번 설명
퀵소트는 최악의 상황에서 소요 시간이 많은 알고리즘입니다.
문제는 오름차순 정렬에서 k번째 index 요소를 출력하라 이고, 새로운 예제로 다음과 같은 입력을 받았다고 가정하겠습니다.
예제
5 2
5 4 3 2 1

A번 설명에서 말한 pivot을 정한 후, 동일하게 순서를 이어나가보겠습니다.
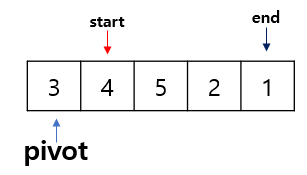
처음 시작과 같이 0번 index와 pivot index를 교환한 후 two pointer를 이용하여 값을 구해보겠습니다.
end의 긴능은 pivot보다 작은 값을 발견하는 것 입니다.
왜냐면 오른쪽에는 큰 값만 들어와야 했었잖아요?
따라서 end는 바로 멈추게 됩니다.
마찬가지로 start는 pivot보다 큰 값을 발견하는 것 입니다.
따라서 start도 바로 멈추게 되는 것 이죠.
이때는 start와 end가 역전되지 않았기에 end와 start를 swap 해 줍니다.

옮긴 start와 end는 각각 pivot보다 작고 큰 것을 검사하였기 때문에, 이 다음만 검사하면 3보다 큰지 작은지는 정렬되게 됩니다.
방금 위치에서 start와 end의 포인터를 증감(++)하여 옮겨 줍시다.

이 지점도 이전과 동일한 상황입니다.
따라서 swap 해 줍시다.

이전과 마찬가지로 증감되었기 때문에, start와 end가 역전이 됩니다.
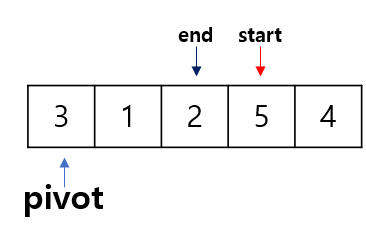
이렇게 역전이 되면서 반복문은 종료되고, end 자리와 pivot 자리가 swap 됩니다.
B-2번 설명

여기서 봤을 때, 아직 정렬이 안된 것 같습니다.
따라서 k번째 자리는 아직이기 때문에 계속 분할하여 정렬하고 찾아내야 합니다.
이제 두개로 분열 할 시간입니다.
현재 3의 좌우로 크고 작은 정도만 정렬했지만, 찾고자 하는 index는 2번이죠?
따라서 3의 왼쪽만 찾아내면 됩니다.

그렇기에 다음과 같은 코드가 존재합니다.
else if (k < pivot)
{
quickSort(a, s, pivot - 1, k);
}
else
{
quickSort(a, pivot + 1, e, k);
}